第1回 平均気温の上昇 その1
年々、暑い時期が長くなり、秋冬が短くなる(二季化)印象を受けますが、実際はどうなのか、平均気温の変化から検討してみます。
今回は「京都」の1974年から2024年の平均気温データを使用します。
データの準備
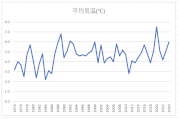
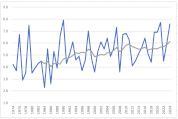
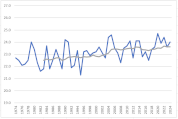
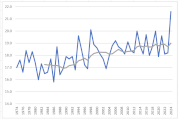
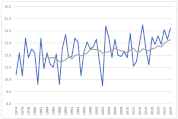
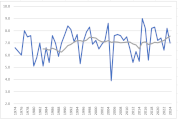
グラフを作成
まとめ
グラフの縦横比がバラバラだと印象が変わり、正しく比較できませんので、各月のグラフの軸の目盛線の数が同じになるようにしましょう。
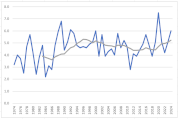
移動平均を算出し、時系列データの傾向をみると、緩急の差はありますが、すべての月で右肩上がりであることが見て取れます。
第1回 平均気温の上昇 その2
年々、暑い時期が長くなり、秋冬が短くなる(二季化)印象を受けますが、実際はどうなのか、平均気温の変化から検討してみます。
その1では気象庁サイトからデータを入手し、各月のシート作成のうえ折れ線グラフを作成し、すべての月で平均気温が右肩上がりであることを確認しました。
データは「京都」の1974年から2024年の平均気温を使用しています。
STEP_1 レンジを調べる
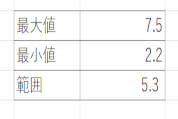 レンジ(範囲)を求め、各月のデータがどれくらいの範囲で広がっているかを確認します。
レンジ(範囲)を求め、各月のデータがどれくらいの範囲で広がっているかを確認します。
まずMAX関数で最大値を出し、MIN関数で最小値を出します。最大値から最小値を引いたのがレンジ(範囲)です。
この期間における各月の平均気温の変動の大小が見えてきます。
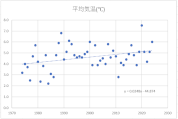
STEP_2 散布図の作成
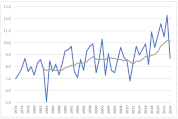
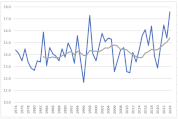
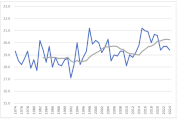
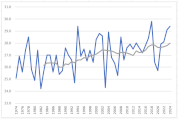
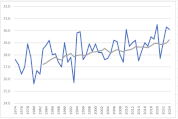
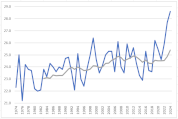
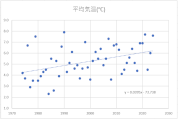
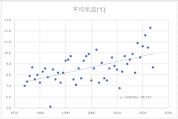
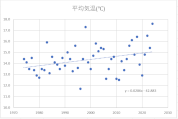
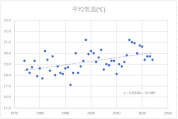
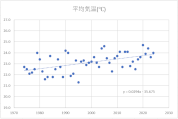
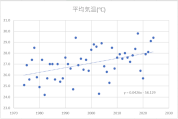
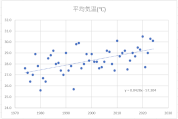
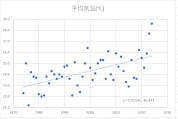
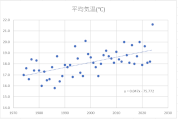
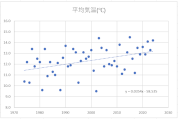
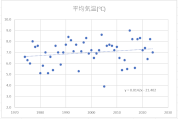
各月の散布図を作成します。折れ線グラフ作成時と同じく、縦横比は同じにしておきましょう。
散布図に近似曲線を挿入し、数式を表示します。
y=ax+bという一次関数です。
今回の場合、x(横軸)は年、y(縦軸)は平均気温ですので、a(傾き)は「年代が進むことで平均気温はどのような影響を受けているか」を表します。
すべての月でa(傾き)はプラスの値ですので、1年進むごとにaの値で平均気温が上昇していることが確認できます。
STEP_3 上位3項目と下位3項目を調べる
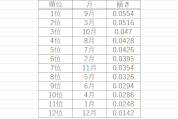
 各月のこの期間における、平均気温の高いほう3位までの年と、低いほう3位までの年を出してみましょう。
各月のこの期間における、平均気温の高いほう3位までの年と、低いほう3位までの年を出してみましょう。
条件付き書式の上位下位ルールを使って、上位3項目と下位3項目に色付けします。
STEP_4 順位表を作成

高いほう1位から3位と低いほう1位から3位を一つの表にまとめます。
2000年を境にして色分けしてみましょう。条件付き書式のセルの強調表示ルールを使います。
高いほうは1999年以前が23.1パーセント、2000年以降は76.9パーセントです。 逆に低いほうは1999年以前が82.9パーセント、2000年以降は17.1パーセントです。
まとめ
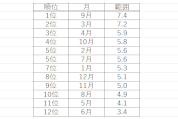
STEP_1から「範囲の大きい順位表」を作成します。
STEP_2から「傾きの大きい順位表」を作成します。
STEP_4の順位表からさらに2020年以降を抽出してみましょう。
ここまでデータを分析し検証してきて、「どういうことが言えるのか」皆さんそれぞれで考えてみましょう。
次回、考察をします。
第1回 平均気温の上昇 その3
年々、暑い時期が長くなり、秋冬が短くなる(二季化)印象を受けますが、実際はどうなのか、「京都」の1974年から2024年の平均気温データを使い、その1とその2で検討してきました。
その結果から、今回は考察をします。
今回はじめてご覧になっているかたは、先に「前回の実例」をお読みください。
WindowsPCの場合、Ctrlキーを押しながら、サイドの「前回の事例」バナーをクリックしていただくと、別ウインドウで表示されます。
STEP_1 平均気温上昇月の考察
まず、範囲の大きい順位、傾きの大きい順位ともに1位は9月、2位は3月であることに注目します。
レンジが大きい、範囲が広がっているということは気温の変動が大きいということです。
また、プラスの傾きが大きい、急な右肩上がりということは、近年平均気温が上昇しているということです。
ここで順位表の高いほうを見ると、9月、3月ともに1位2位は2020年以降です。
9月と3月は約50年の間で気温の上昇が比較的急だと考えられます。
特にここ数年が顕著なようです。
併せて10月についても、範囲の大きい順位が4位、傾きの大きい順位が3位ですので、気温上昇の傾向が見られます。
STEP_2 変化の少ない月の考察
次は、範囲の大きい順位、傾きの大きい順位の下位を見てみましょう。
12月と1月に注目してみます。
傾きの大きい順位の12位と11位ですので、気温の上昇が緩やかと言えます。
範囲の大きい順位でも、8位と7位で平均気温のばらつきも比較的せまいです。
つまり、冬の寒さは約50年間でさほど変わっていないということです。
また、6月と5月は範囲の大きい順位12位と11位で、平均気温の変動が少ないですし、傾きも割と緩やかです。
初夏や梅雨時期はあまり変わっていないようです。
STEP_3 イメージしやすく
 ここまでの考察で、「冬の寒さは変わっていないが、春先と初秋の気温は上昇傾向」といえるのではないでしょうか。
ここまでの考察で、「冬の寒さは変わっていないが、春先と初秋の気温は上昇傾向」といえるのではないでしょうか。
秋から冬に向かうところで、気温が大きく下がる印象を受ける理由づけになったと思います。
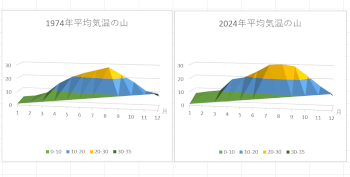
1974年と2024年の1年間の平均気温を山にしてみました。
絵にしてみると、イメージしやすいですし、伝わりやすくなります。
1974年のほうが山が低く、稜線が左右とも割となだらかです。
2024年のほうは山が高く、向かって左側が階段状になっており、右側は1974年に比べ急斜面です。
まとめ
二季化というと、春と秋がなくなって夏と冬の二つの季節になると思われるのですが、今回の考察からは、秋と冬が短くなり、春と夏が長くなっていると考えられます。
今のところ、秋が短くなり3.5季くらいではないでしょうか。
ただ、今回の考察はあくまでも京都の約50年の平均気温の話ですので、最高気温や最低気温、日照時間など他の要素、また他の地域では異なる結果が出るかもしれません。
ぜひ、ここを第一歩として、様々な角度、切り口で考察を広げていってください。
当サイトでも、また機会を改めて違う角度から考察してみたいと思います。
記事作成 2025年8月-2025年11月